Spectral graph theory and algorithms
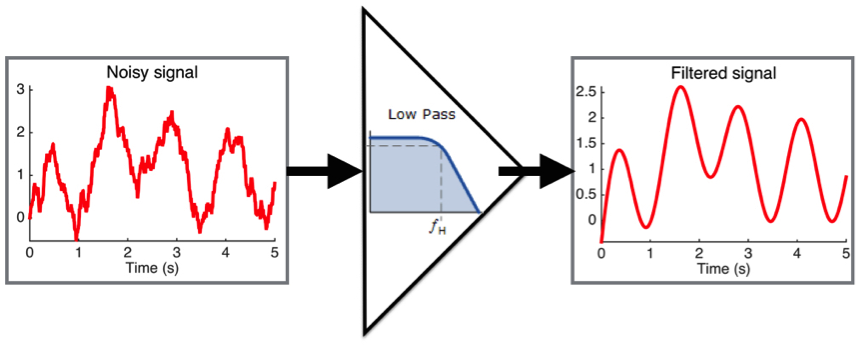
Traditional signal-processing is based on the idea that the information is supported on a regular structure. For example, the noisy records of a single sensor over time rely on a very strong structure: “time”. Building hypotheses like “The signal shall not change too quickly” on this structure, we can design algorithms to enhance our measurements by removing the noise (with a low-pass filter for example (See Figure 1)).
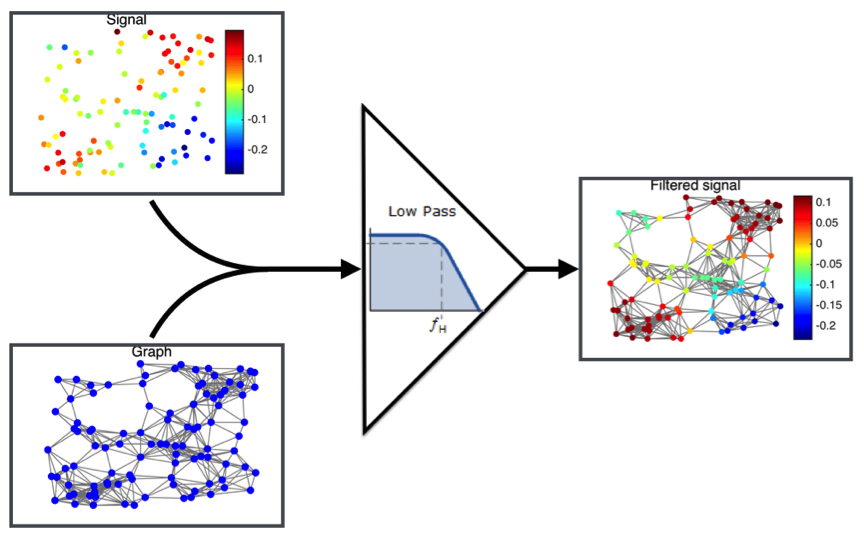
However, in many cases the information does not have a regular structure. For instance, imagine that instead of having only one temperature sensor, we have many placed at different random points in the space. Instead of time, the structure here is the space. However, it is irregular because the sensors are not distributed on a grid. In this case, the solution is to create a graph that would capture the structure of the data. To do this, we connect the nearest sensors together. The connections model the fact that close sensors should have similar values because the temperatures cannot change abruptly in space. With this construction, we can use a graph algorithm to remove the noise of the sensor array (See Figure 2).
Signal-processing on graphs
Graph signal processing is a special area in signal processing based on spectral graph theory where the data possess an intrinsic graph structure. Social networks are one of the most common examples of such data since the graph is simply provided by the users themselves. Nevertheless, most of the time this does not happen and the graph is constructed directly from the data or from additional information. The graphs are usually used to discretize the abstract domain of the data and build accurate representations of them. Common tasks in signal-processing on graphs include filtering, de-noising, in-painting, compression, clustering, partitioning, sparsification, features extraction, classification and regression. Almost all signal-processing tools have been generalized to graphs, thus allowing them to be used on irregular data structures. The range of applications cannot be enumerated but contains, among others, automatic text classification, Internet page ranking, digit classification and movie recommendations.
Personal contributions
- Data probabilistic model: Generalizing the concept of stationarity on graphs, we propose a new model for data. This model is able to exploit the intrinsic links between the features and show very exciting results. PDF Code
- Local uncertainty principle: The structure of the graph being far from regular, we propose the new concept of local uncertainty principle. Instead of a single number, our uncertainty bound is a function evolving on the graph providing insights of the graph structure. PDF
- DeepSphere: Leveraging graph convolution neural networks, we have defined a new deep neural network architecture designed for spherical data. PDF Code
- Graph signal processing toolbox: The graph signal processing toolbox is an open-source collection of algorithms combining my research with that of my co-workers. It contains efficient implementations of graph filtering operations that allow a rapid computation of the wavelet or Gabor transform. Available in MATLAB and Python, it is fully documented and provides a tutorial and some demonstration files. Website
- Graph signal prossessing of time series: Graphs are very convenient tools to model the structure behind multivariate time series. We have been developing the basic tools for the analysis of such signals through multiple contributions. PDF PDF PDF PDF PDF
- Large scale graph learning: Leveraging convex optimization and graph signal processing, we show how to scale the graph learning problem. PDF Code
- Fast filtering algorithm: Graph filtering is the base of many algorithms. To use it on big datasets and overcome the curse of dimensionality, we have developed a novel fast-filtering algorithm. Based on Lanczos’ polynomial approximation, it allows us to accurately and efficiently apply any filtering operations on graphs. This algorithm is particularly efficient when the data structure is very irregular. PDF Code