Deep Learning
Deep learning has recently become one of the hottest topics in machine learning. Originally inspired by the brain and the connections between neurons, the first deep learning algorithm had multiple layers of computational units. In that case, the learning task consisted of inferring the connectivity patterns between the neurons. The problem was formulated as a big non-convex optimization problem and was solved mainly using advanced gradient descent techniques. Deep learning has only become popular in the last few years as computers became powerful enough to solve those complex problems efficiently, while at the same time researchers have elaborated techniques to solve computational issues, such as the vanishing gradients. Additionally, the adoption of GPUs has allowed us to solve those big problems on personal computers quite efficiently.
Selecting the adequate architecture
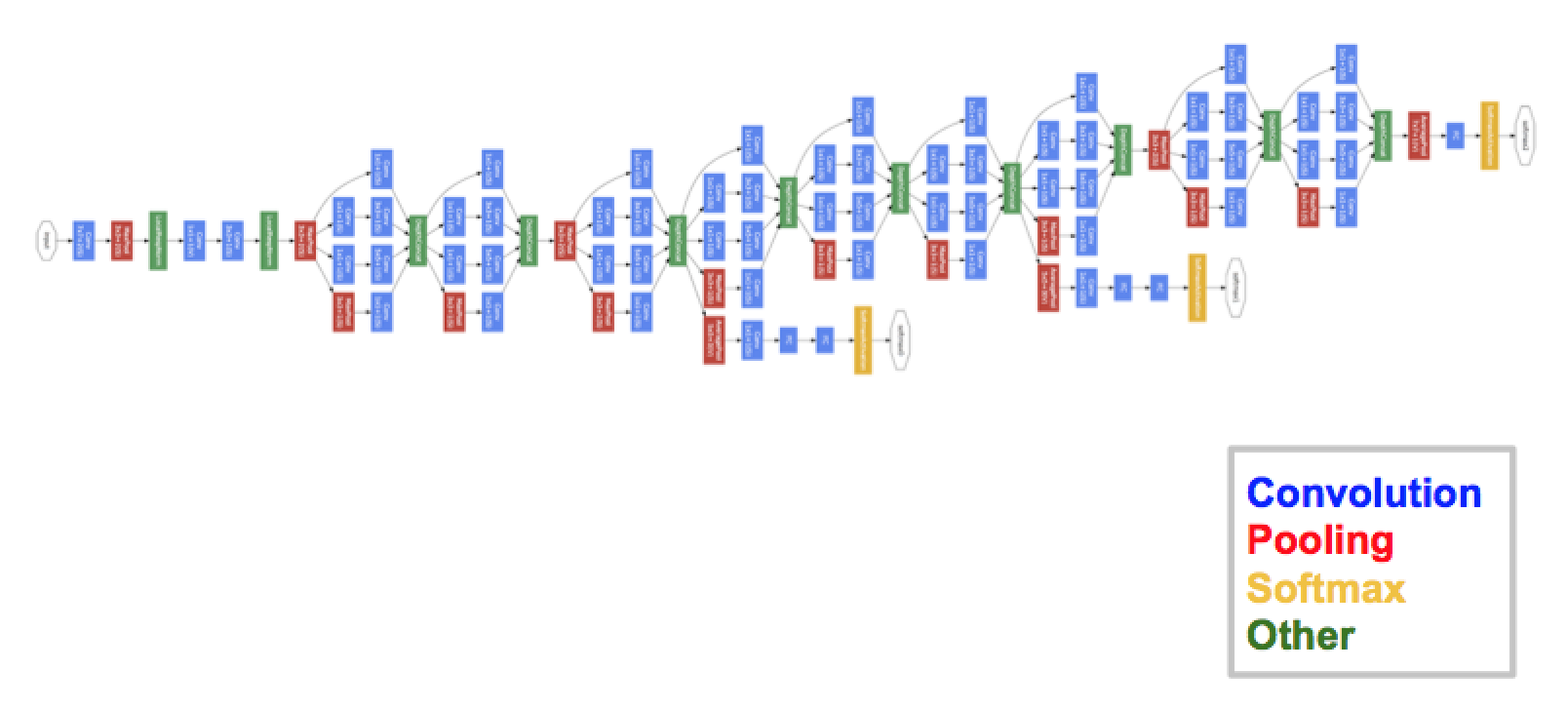
In linear regression, one searches for the line that best fits a collection of points by adjusting its intercept and slope. Similarly, in deep learning, we search for the optimal parametrization of a sophisticated function composed by several operations also called "layers." One of the fundation of deep learning is to trade a large number of layers and parameters and hence more expressivity in the regression model for a larger training dataset. Nevertheless, one has to keep in mind that deep learning is usually successful when the network architecture accommodates data characteristics. For example, convolutional neural networks (CNNs) revolutionized computer vision because the network architectures have been specifically designed to deal with images and general 2D signals. CNNs have two key advantages. a) They are built for translation equivariance, meaning that if the input is translated, so will the output. This property helps to encode hypothesis such as "the properties of an object should not depend on its absolute position." b) From an optimization perspective, convolution is efficient as it benefits from high parallelization on GPUs, while also significantly reducing the number of parameters compared to a matrix multiplication. Hence CNNs allows for very deep architectures made of many layers such as GoogleNet/Inception (See Figure 1).
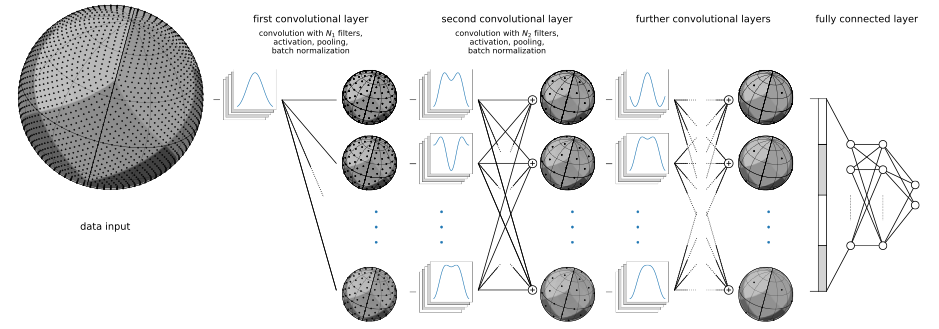
I am particularly interested in generalizing convolutional neural networks to irregular data domain. For example, in augmented reality scenarios, we will have to deal with 360° images, or images projected on spherical domains. With my colleagues of EPFL and ETHZ, we developed a special architecture for spherical images called DeepSphere (See Figure 2). You can learn more about it by reading this blogpost.
Generative modeling
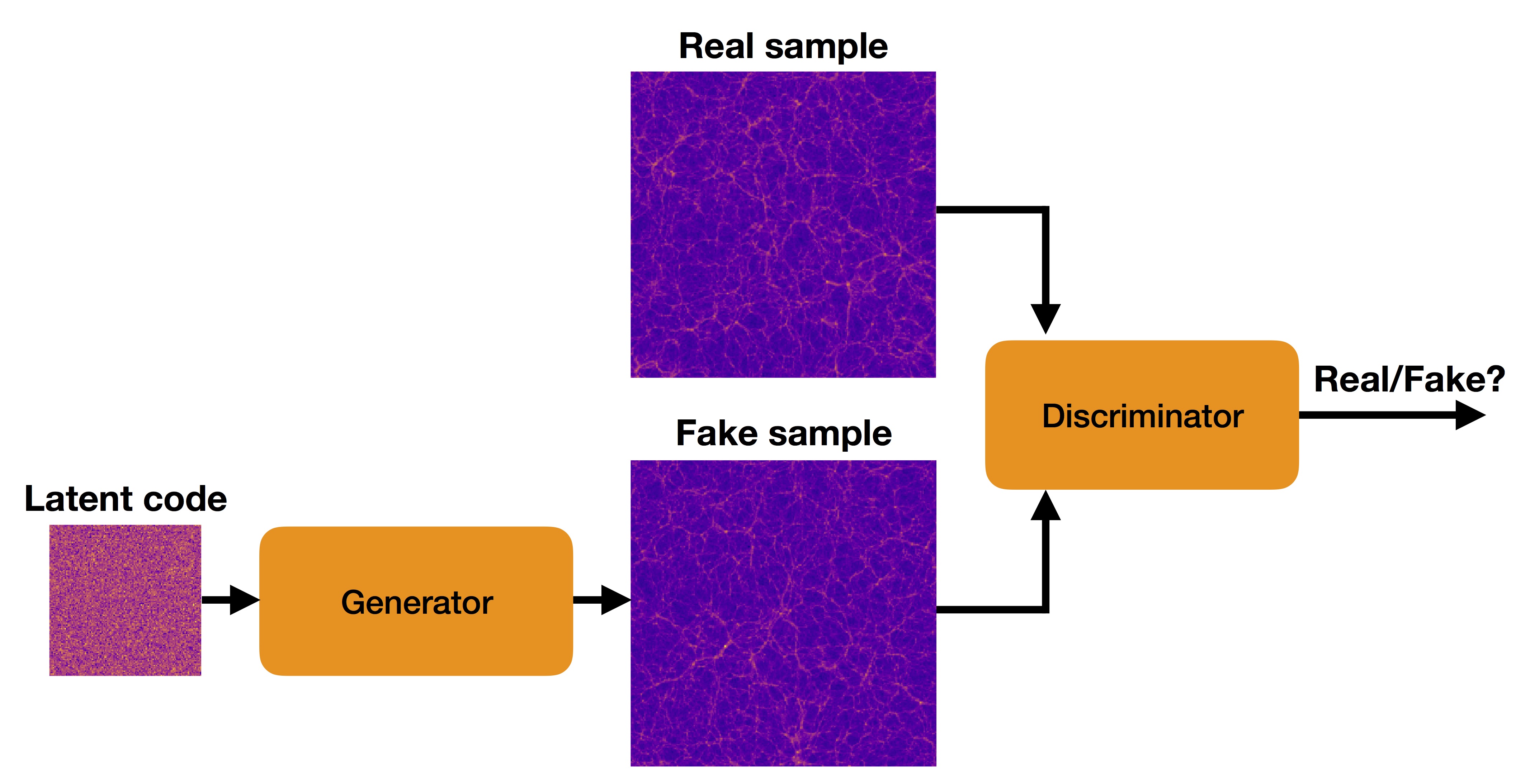
I am currently working with generative adversarial networks (GANs) that are a class of machine learning algorithms relying on two neural networks, a generator and a discriminator. cThey are trained by setting up a competition with each other, formulated as a zero-sum game. As depicted in Figure 3, the generator produces fake samples and attempts to "fool" the discriminator by making them as realistic as possible. Simultaneously, the discriminator learns to discriminate between the real and generated samples. Providing both networks are trained correctly, they learn from each other until the generator produces samples that are, in theory, indistinguishable from the real ones.
This technique allows for learning the data distribution from a collection of samples. Hence it can be used to generate samples of the modeled data, such as realistic sound or images. In my research, I particularly use GANs for two applications. The generation of Nbody simulation (Cosmology) and the generation of sound.
Personal contributions