Optimization
Optimization is a field of mathematics where the goal is to select the best element with respect to criteria from a set of available alternatives. Put this way, it resembles a mathematician’s playground. However, optimization is at the heart of many algorithms. It is used to answer direct questions like: What is the best financial investment that I can make? What is the best shape for this component? Where is the safest place to live? It is also used indirectly. Many machine-learning algorithms require solving an optimization problem and many problems can be reformulated as optimization problem. For instance, “How to recover missing values?” can be expressed as “What is the best way to recover the missing values?”
How is optimization used?
Optimization is never the purpose, but only a solution part of a problem. Hence, when one has to solve a problem, the first step is to model it (express the mathematical form) thanks to knowledge in machine learning, signal processing or statistics. The second step is to select the right algorithm. Figure 1 illustrates the two steps.
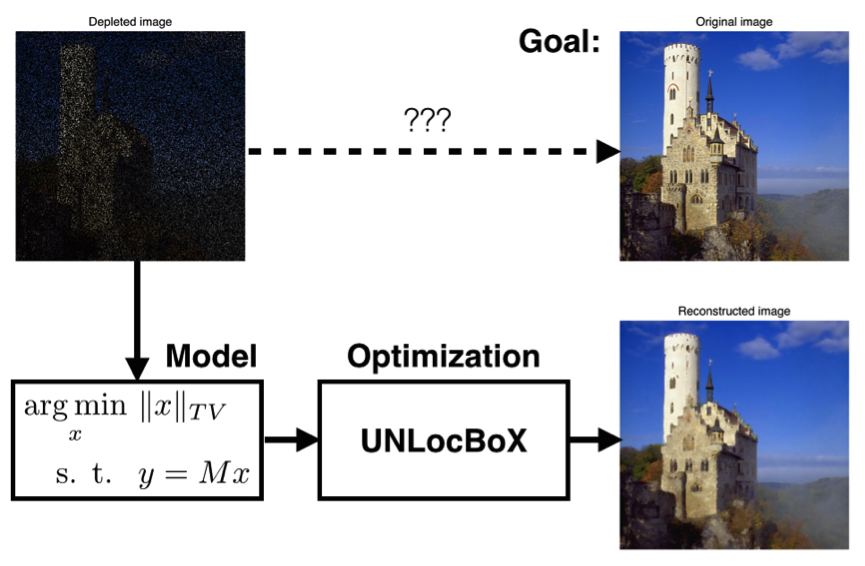
Modelization(formulation of the problem)
The conception of the model is a creative step where we transform our requirements into mathematical equations. There is usually a trade-off between the accuracy and the complexity (the more accurate the model, the more complex). Modelization also includes the final design of the problem. The same model can usually be expressed with different mathematical formulations. However, some may be much easier to solve than others. A clever choice can make the difference between what is solvable and unsolvable. This competence is mostly acquired with experience.
Optimization (solving the problem) - UNLocBoX
Optimization was so omnipresent during my thesis that I have developed my own software. The UNLocBoX is a convex optimization toolbox written in MATLAB and ported to Python (PyUNLocBoX). It is capable of solving large non-smooth problems, is based on proximal-splitting methods and includes the most recent efficient algorithms.
While this software is very useful for traditional machine learning and signal processing algorithms, it is not designed for optimization of deep architectures. Hence, today my research relies mostly on traditional optimizers present in TensorFlow and PyTorch.